Day 8: Epsilon Delta Limit Examples/Problems/Proofs and Explanations

This point of this post is to introduce the definition and procedure of epsilon delta proofs of limits. First an explanation and then several problems.

What is a limit? 
Thinking purely conceptually, we think about it as a final goal on the path, whether we're travelling from the left or travelling from the right--the path is the function. This is certainly equivalent to saying, for every positive error, epsilon, there exists a positive delta such that if:
.
This probably sounds like a bunch of jargon right now, but by thinking intuitively what a limit is and means will make proving these possible. Let's state the formal definition and break it down into parts.





So, from the top, it says "for all", meaning no matter what error epsilon we choose there is always a corresponding delta to choose that makes the following implication true: If minus delta is less than the distance from a to x, where x is a number close to a, is the less than delta, then minus epsilon is less than the distances from L to f(x) is less than epsilon. IF AND ONLY IF (i.e. LOGICALLY EQUIVALENT TO:) the limit as x goes to a of f(x) is equal to L. So all we're really doing with this junk is PROVING a limit, since this is merely a definition.

Let's illustrate a limit graphically, using epsilon and delta: 
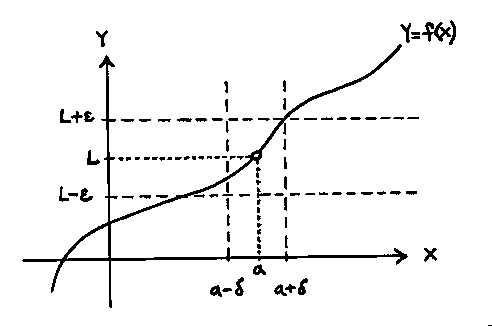
So when f(x) is within epsilon of the limit, L, then x is within delta of what the limit is approaching, a.
Hence, the limit is true.

Let's look at some examples now:

(easy)

So we wish to show that for all epsilon greater than zero, there exists delta such that if |x-1|<delta, then |f(x)-2|<epsilon.

So let's consider a random epsilon. what would the corresponding delta have to be to make the above implication true?